Leonardo Fibonacci, figlio di Guglielmo Bonacci, nacque a Pisa intorno al 1170. Suo padre era segretario della Repubblica di Pisa e responsabile a partire dal 1192 del commercio pisano presso la colonia di Bugia, in Algeria. Alcuni anni dopo il 1192, Bonacci portò suo figlio con lui a Bugia. Il padre voleva che Leonardo divenisse un mercante e così provvide alla sua istruzione nelle tecniche del calcolo, specialmente quelle che riguardavano le cifre indo-arabiche, che non erano ancora state introdotte in Europa. In seguito Bonacci si assicurò l’aiuto di suo figlio per portare avanti il commercio della repubblica pisana e lo mandò in viaggio in Egitto, Siria, Grecia, Sicilia e Provenza. Leonardo colse l’opportunità offertagli dai suoi viaggi all’estero per studiare e imparare le tecniche matematiche impiegate in queste regioni. Intorno al 1200, Fibonacci tornò a Pisa dove per i seguenti 25 anni lavorò alle sue personali composizioni matematiche. In tutta la sua produzione l’opera più importante è il "Liber abaci", comparso attorno al 1228: è un lavoro contenente quasi tutte le conoscenze aritmetiche e algebriche ed ha avuto una funzione fondamentale nello sviluppo della matematica dell’Europa occidentale. In particolare la numerazione indo-arabica, che prese il posto di quella latina semplificando notevolmente i commerci extraeuropei, fu conosciuta in Europa tramite questo libro. In tale sistema di numerazione, il valore delle cifre dipende dal posto che occupano: pertanto egli fu costretto ad introdurre un nuovo simbolo, corrispondente allo zero "0", per indicare le posizioni vacanti. La reputazione di Leonardo come matematico divenne così grande che l’imperatore Federico II gli chiese un’udienza mentre era Pisa nel 1225. Dopo il 1228 non si sa in sostanza niente della vita di Leonardo tranne il decreto della Repubblica di Pisa che gli conferì il titolo di "Discretus et sapiens magister Leonardo Bigollo" a riconoscimento dei grandi progressi che apportò alla matematica. Fibonacci morì qualche tempo dopo il 1240, presumibilmente a Pisa. Anche al giorno d’oggi la fama di Leonardo è tale che esiste un’intera pubblicazione dedicata ai suoi numeri: il "Fibonacci Quarterly", periodico matematico dedicato interamente all’aritmetica connessa alla sequenza di Fibonacci.
La successione di Fibonacci, è una sequenza di numeri interi naturali ottenuti ognuno dalla somma dei due termini precedenti della sequenza Fn = Fn-1 + Fn-2. I due valori iniziali della sequenza sono uguali a F0= 1 ed F1= 1.
Essa nasce come soluzione proposta da Fibonacci per un problema che lui stesso riporta nel Liber Abaci del 1228:
Ci sia una coppia di conigli il primo gennaio, questa coppia generi un’altra coppia di conigli il 1° febbraio e così via per tutti i mesi dell’anno il primo giorno di ogni mese. Ciascuna nuova coppia produce a sua volta una coppia di conigli il primo giorno di ogni mese a partire dal secondo mese di vita e così via. Si domanda quante coppie di conigli ci saranno alla fine dell’anno.
Il primo mese la prima coppia genera la seconda coppia discendente e così dopo un mese ci saranno due coppie di conigli, al secondo mese avremo tre coppie perché solo la prima ha generato un‘altra coppia, al terzo mese ne avremo cinque in quanto le prime due coppie ne hanno generato una ciascuna e così al quarto mese ne avremo otto e così via secondo la tabella qui riportata:
Qui di seguito il diagramma ad albero che mostra il numero di coppie di coniglio per ogni anno
I primi 41 numeri di Fibonacci sono:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 , 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765 , 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155
I numeri di Fibonacci godono di una gamma stupefacente di proprietà, si incontrano nei modelli matematici di svariati fenomeni e sono utilizzabili per molti procedimenti computazionali. Passiamo in rassegna adesso alcune proprietà di questi numeri. Supponiamo di voler calcolare la somma di un numero qualunque di termini della successione di Fibonacci ( prendendo i termini in ordine e senza salti ):
1+1= 2 = (3-1)
1+1+2 = 4 = (5-1)
1+1+2+3 = 7 = (8-1)
1+1+2+3+5 = 12 = (13-1)
…………………………….
Osservando i valori ottenuti, concludiamo che la somma di un certo numero di termini della successione di Fibonacci è sempre uguale al termine che segue di due posti l’ultimo termine, diminuito dell’unità. In formule
F1+F2+….Fn=Fn+2 - 1
Così per la somma dei termini di posto dispari:
1 1 2 3 5 8 13 21 34 ………
avremo:
1 = 1
1+2 = 3
1+2+5 = 8
1+2+5+13 = 21
…………………
Quindi in formule:
F1+F2+…..+F2n-1=F2n
Per la somma dei termini di posto pari:
1 1 2 3 5 8 13 21 34 ………….
avremo:
1 = 1 = (2-1)
1+3 = 4 = (5-1)
1+3+8 = 12 = (13-1)
1+3+8+21 = 33 = (34-1)
…………………………..
cioè F2+F4+….+F2n=F2n+1 - 1
Consideriamo, adesso, la somma dei quadrati dei termini della successione di Fibonacci. Poiché
avremo in generale:
F12+F22+….+Fn2=(Fn* Fn+1)
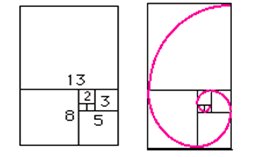
Se interpretiamo geometricamente la relazione qui scritta, possiamo osservare, che un rettangolo di lati a , b , proporzionali a due numeri consecutivi di Fibonacci è esauribile per successiva iscrizione di quadrati. Questi quadrati hanno il lato di misura diversa, esclusi i due più piccoli che hanno entrambi il lato di misura unitaria.
All’interno dei quadrati e’ possibile inserire una spirale disegnando un quarto di cerchio. La spirale non e’ una vera e propria spirale nel senso matematico (in quanto e’ fatta di frammenti che sono parte di cerchi ) ma e’ una buona approssimazione delle spirali che appaiono molto spesso in natura. Si possono ammirare nelle forme dei gusci delle lumache e delle conchiglie di mare (vedi Figura 1) come anche per particolari gruppi di galassie del nostro universo dette appunto galassie a spirali (vedi Figura 2).
Figura 1. Immagini di conchiglie di Nautilus.
Figura 2. Galassia a spirale M51 nella costellazione dei Cani di caccia.
Altre spirali di Fibonacci si possono trovare nelle pigne. In esse sono presenti due arrangiamenti di spirali che crescono andando verso l’esterno del frutto, partendo dal punto in cui esse sono attaccate ai rami (vedi Figura 3).
Figura 3. Nella pigna rappresentata al centro della figura ci sono 8 spirali che vanno verso la punta della pigna in senso orario. Nella figura di destra invece viene riportata una delle 13 spirali che si sviluppa in senso antiorario.
Sorprendente no? Ma non e’ finita qui. Avete mai provato a guardare il centro di una margheritina fiorita, durante qualche vostra passeggiata primaverile? No? Allora osservate la Figura 4 e vedrete cosa la Natura riesce a fare utilizzando la matematica di Fibonacci.
Figura 4. La corolla di una margherita fiorita. Ci sono 21 spirali antiorarie e 34 orarie.
Molto probabilmente la maggior parte di noi non ha avuto mai tempo per esaminare attentamente il numero o l’arrangiamento dei petali di un fiore. Se l’avessimo fatto avremmo avuto la sorpresa di vedere in azione i termini della sequenza di Fibonacci (Figura 5 e 6).
Fiori con un petalo e due petali non sono molto comuni mentre lo sono di più quelli con 3 petali. Ci sono, invece, centinaia di specie sia selvagge che coltivate con 5 petali. Fiori con otto petali non sono così comuni come quelli con 5 ma sicuramente sono più di quelli con 1 e 2 petali.
Figura 5. Fiori con 1, 2, 3, 5, 8, 13 petali.
Figura 6. Fiori con 21 e 34 petali.
Ci sono fiori con 13 petali e quelli con 21 e 34 che anche sono molto comuni. Esistono poi margherite che hanno addirittura 55 o 89 petali. Veramente incredibile. C’e’ da dire comunque che alcune specie hanno esattamente il numero di petali corrispondenti a numeri di Fibonacci, mentre altre hanno un numero di petali molto vicino ai numeri di Fibonacci e che quindi seguono tali numeri solo in media.
E non finisce qui. La Natura continua a stupirci nell’usare i numeri di Fibonacci. Qui riportiamo un altro esempio analizzando la disposizione di alcune foglie intorno agli steli delle piante. Se guardiamo una pianta dall’alto verso il basso scopriremo che spesso le foglie sono arrangiate in modo da evitare che quelle superiori coprano quelle inferiori. Questo per garantire che ogni foglia riceva una buona quantità di luce e riesca a veicolare una buona quantità di acqua piovana verso le radici.
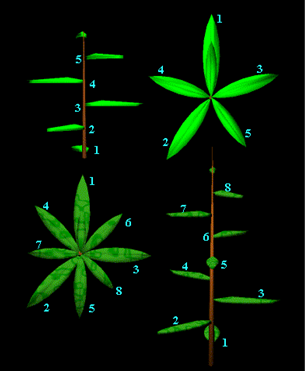
I numeri di Fibonacci si manifestano quando contiamo sia il numero di volte che giriamo intorno allo stelo muovendoci di foglia in foglia, sia quando contiamo il numero di foglie che incontriamo fino alla foglia che si trova direttamente al di sopra di quella da cui siamo partiti. Se invece contiamo nell’altra direzione otteniamo un numero diverso di giri per lo stesso numero di foglie. Il numero di giri in ogni direzione e il numero di foglie incontrato corrisponde a 3 numeri di Fibonacci consecutivi. Per esempio per la pianta riportata in alto della Figura 7 dobbiamo effettuare 3 rotazioni orarie prima di incontrare una foglia direttamente sopra la prima e aver visitato 5 foglie. Se invece, ci muoviamo in senso antiorario, abbiamo bisogno di solo 2 giri.
Ormai abbiamo imparato a riconoscerli: 2, 3 e 5 sono numeri di Fibonacci consecutivi. Per la pianta invece riportata in basso della Figura 7 abbiamo 5 rotazioni in senso orario con 8 foglie tra la prima e l’ultima e 3 rotazioni nell’altro senso. Questa volta ci sono altri tre numeri di Fibonacci consecutivi: 3, 5 e 8.
Le piante analizzate sono state prodotte con il computer e quindi qualcuno potrebbe essere portato a pensare che in Natura le cose non stiano esattamente così. Niente di più sbagliato. I botanici hanno stimato che circa il 90% di tutte le piante in Natura esibisce una disposizione delle foglie che segue la sequenza di Fibonacci.
Figura 7. Disposizione delle foglie per piante virtuali generate al computer
Tutto cio’ sembra portarci a pensare che in Natura i numeri di Fibonacci siano una legge Naturale. Ma questo non e’ vero. Ci sono esempi di piante, fiori o frutti, che non seguono la sequenza di Fibonacci. Anche se queste discrepanze danno fastidio ai botanici moderni così non e’ per i devoti di Fibonacci per i quali il fenomeno anche se non e’ una legge e’ almeno un’affascinante tendenza della Natura. Qual’e’ il motivo per cui i numeri di Fibonacci sono così comuni in Natura? La risposta e’ che questo fenomeno potrebbe essere un’espressione dell’efficienza della Natura. Man mano che una riga di semi in un girasole o la riga di squame in una pigna crescono radialmente allontanandosi dal centro, lo fanno perche’ la natura cerca di disporre il massimo numero di semi (o di squame) nello spazio più piccolo. Quindi la sequenza di Fibonacci esprime l’impacchettamento dei semi nello spazio disponibile più efficiente a disposizione della Natura.
Un altro aspetto importante della sequenza di Fibonacci e’ legato al problema dei conigli già riportato precedentemente. Consideriamo la figura 8 dove ogni immagine grande rappresenta un coniglio adulto e quella piccola un coniglio giovane.
I conigli piccoli vengono riportati a destra del loro genitore e la sequenza procede verso destra. La disposizione dei conigli adulti (A) e quelli giovani (b) può essere scritta come:
AbAAbAbAAbAAbAbAAbAbA ......
Figura 8. Sequenza geometrica dei conigli di Fibonacci. Il coniglio grande rappresenta una coppia di adulti mentre quello piccolo un giovane
Questa sequenza di A e b e’ deterministica nel senso che essa si estende all’infinito in modo unico e prevedibile. In questo senso e’ diversa da una sequenza casuale dove ogni termine non e’ prevedibile. Ma e’ diversa anche da quella che viene chiamata una sequenza periodica. Un semplice esempio di sequenza periodica e’:
AbAbAbAbAbAbAbAbAbAb .......
dove la stringa Ab si ripete all’infinito. Ci sono due importanti caratteristiche per una sequenza periodica:
1) una più ampia porzione della sequenza può essere generata ripetendo una più piccola porzione, in questo caso Ab, AbAb, AbAbAb etc…
2) queste porzioni più piccole della sequenza hanno lo stesso rapporto di A e b di porzioni più lunghe.
Come si può facilmente provare nessuna di queste due proprietà e’ soddisfatta dalla sequenza di Fibonacci. Per questo motivo la sequenza e’ detta quasi periodica essendo prevedibile ma non periodica. E’ tutto per il momento.